Recursion
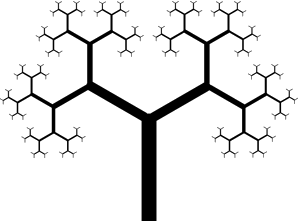
Recursion, in a mathematical context, refers to a repeated procedure in which each step that is produced relies on, builds on, the results of the previous step. In other words, recursive objects are defined in term of themselves (according to a particular rule). The fractal tree above is an example of an object made by a recursive procedure.
For the purposes of the paper this site accompanies, these definitions are too abstract. I invite you to scroll down the page and discover two, more in-depth, examples.
The Sierpinski Triangle
... is a fractal. A fractal is an object, either produced by nature or by a mathematical set, that is composed of a repeating pattern visible at any scale.
The construction of the object is the most important aspect, as therein lies the recursive process. Each stage grows from the previous one; the same rule is applied every time: take each triangle, divide into four smaller triangles and remove the center one.
A tangential but fascinating side note: if this process were to go on indefinitely the triangle would seem to disappear!
Recursive Functions
At the side of this page are two examples of recursive functions: one written in JavaScript, one in English.
The JavaScript function is an example of factorial calculation that uses a recursive method. A factorial is the multiplication of an integer by every number that proceeds it, down to one. If the integer is 5, its factorial would be calculated like so: 1 * 2 * 3 * 4 * 5, which equals 120.
This function takes a given number (n) and multiplies it by itself minus 1 (n-1). The recursive piece of the function comes in this calculation, as the function (called 'factorial') uses itself to complete the calculation. On the line "return n * factorial(n-1)" the function essentially restarts with the new value (n-1), and will repeat the process until n = 0.
The English example, while it lacks internal logic, demonstrates a key facet of recursion as a method in computer science; we start with a problem (or set of data), build on it until a resolution is reached, and then solve the original problem from the inside out.
For our purposes, the most important factor in both of these examples is that any progress made, any resolution eventually gained, is non-linear. The eventual success of the functions is based on revisiting and revising old data. In recursive methodology, progress and regress are unavoidably interdependent.
An example of a recursive function
function factorial(n) {
if (n === 0) {
return 1;
}
return n * factorial(n - 1);
}
Recursion, as explained by a, possibly, mythical Computer Science Professor
A child couldn't sleep, so her mother told her a story about a little frog,
who couldn't sleep, so the frog's mother told her a story about a little bear,
who couldn't sleep, so the bear's mother told her a story about a little weasel...
who fell asleep.
...and the little bear fell asleep;
...and the little frog fell asleep
...and the child fell asleep.